回転行列
ブロックアウトのピット内に、x軸・y軸・z軸を下記のようにとる。
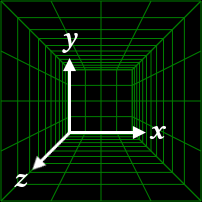
z軸を中心として、x軸からy軸方向にθ回転した場合の座標変換は、下記で表せる。
| = | |||||||||||
| x' | cosθ | -sinθ | 0 | x | |||||||
| y' | sinθ | cosθ | 0 | y | |||||||
| z' | 0 | 0 | 1 | z | |||||||
θ=π/2(90°)と置くと、C回転を表す座標変換となる。
| = | = | = | ||||||||||||||||||||||
| x' | cos(π/2) | -sin(π/2) | 0 | x | 0 | -1 | 0 | x | -y | |||||||||||||||
| y' | sin(π/2) | cos(π/2) | 0 | y | 1 | 0 | 0 | y | x | |||||||||||||||
| z' | 0 | 0 | 1 | z | 0 | 0 | 1 | z | z | |||||||||||||||
同様に、y軸を中心として、z軸からx軸方向にθ=π/2(90°)回転した場合の座標変換が、B回転を表す。
| = | = | = | ||||||||||||||||||||||
| x' | cos(π/2) | 0 | sin(π/2) | x | 0 | 0 | 1 | x | z | |||||||||||||||
| y' | 0 | 1 | 0 | y | 0 | 1 | 0 | y | y | |||||||||||||||
| z' | -sin(π/2) | 0 | cos(π/2) | z | -1 | 0 | 0 | z | -x | |||||||||||||||
ここで、それぞれの座標変換で用いられる回転行列を、C、Bとおく。
| C = | , | B = | ||||||||||
| 0 | -1 | 0 | 0 | 0 | 1 | |||||||
| 1 | 0 | 0 | 0 | 1 | 0 | |||||||
| 0 | 0 | 1 | -1 | 0 | 0 | |||||||
これらの行列式を用いると、回転による座標変換は 「x' = Cx」 のように表せる。
ここで注意すべきは、複数の回転動作による座標変換である。 例えば、BC回転を表す変換は、 「x' = Bx」 「x'' = Cx'」 の連続動作であるため、後者の式に前者のx'を代入することで、 「x'' = Cx' = C(Bx) = (CB)x」 となり、BC回転の回転行列式は「BC」ではなく「CB」となることに注意されたい。 また、行列式は交換法則を満たさないため、「CB=BC」は一般的には成立せず、 このことから、BC回転とCB回転が同値でないことが言える。
CB回転
CB回転の回転行列は「BC」であり、下記のような変換となる。
| = BC | = | = | = | ||||||||||||||||||||||||||||||
| x' | x | 0 | 0 | 1 | 0 | -1 | 0 | x | 0 | 0 | 1 | x | z | ||||||||||||||||||||
| y' | y | 0 | 1 | 0 | 1 | 0 | 0 | y | 1 | 0 | 0 | y | x | ||||||||||||||||||||
| z' | z | -1 | 0 | 0 | 0 | 0 | 1 | z | 0 | 1 | 0 | z | y | ||||||||||||||||||||
これは、回転前のz座標がx座標に、x座標がy座標に、y座標がz座標に置き換わる変換である。